Canonical Quantum Phase Estimation AlgorithmDeterministicQPE

Quantum phase estimation (QPE) is a quantum algorithm used to estimate the phase \(\phi \in [0, 1)\) of a given unitary operator \(U\) and eigenstate \(|\phi\rangle\) satisfying

(23)\[U|\phi\rangle = e^{i2\pi\phi} |\phi\rangle .\]

QPE based on the quantum Fourier transform (QFT) [11, 12, 13, 14] is referred to as canonical QPE. QFT can be considered to be a quantum analogue to the discrete Fourier transform, and is expressed as:

(24)\[|j\rangle \longrightarrow \frac{1}{\sqrt{N}} \sum_{k} \exp\left({i\frac{2\pi jk}{N}}\right) |k\rangle\]

where \(N\) is the total number of states. This general expression can be rewritten with \(n\) qubits as

(25)\[|j_{1}\cdots j_{n}\rangle \longrightarrow \frac{1}{\sqrt{2^{n}}} \left( |0\rangle + e^{i2\pi 0.j_{n}}|1\rangle \right) \otimes \cdots \otimes \left( |0\rangle + e^{i2\pi 0.j_{1}j_{2}\cdots j_{n}}|1\rangle \right)\]

where the binary fraction is represented as \(0.j_{1}\cdots j_{n} = \sum_{k=1}^{n} j_{k} 2^{-k}\). The basic idea of the canonical QPE is to compute the right-hand side of QFT using Eq. (23) and estimate the phase factor as a bit string by the inverse QFT.

To do this, canonical QPE uses two quantum registers. The first register contains \(n\) qubits initially in the state \(|+\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\). The choice of \(n\) depends on the precision of the estimate of \(\phi\) we wish to reach. The second register is initialized in the state \(|\phi\rangle\), and contains as many qubits as is necessary to represent \(|\phi\rangle\).

We compute the right-hand side of (25) using the phase kickback technique:

(26)\[|+\rangle \otimes |\phi\rangle \xrightarrow{\mathrm{ctrl-}U^{2^{k-1}}} \frac{1}{\sqrt{2}}\left( |0\rangle + e^{i2\pi 0.\phi_{n-k+1}\phi_{n-k}\cdots \phi_{n}} |1\rangle \right) \otimes |\phi\rangle\]

The example of the canoncial QPE circuit is shown in Fig. 4.

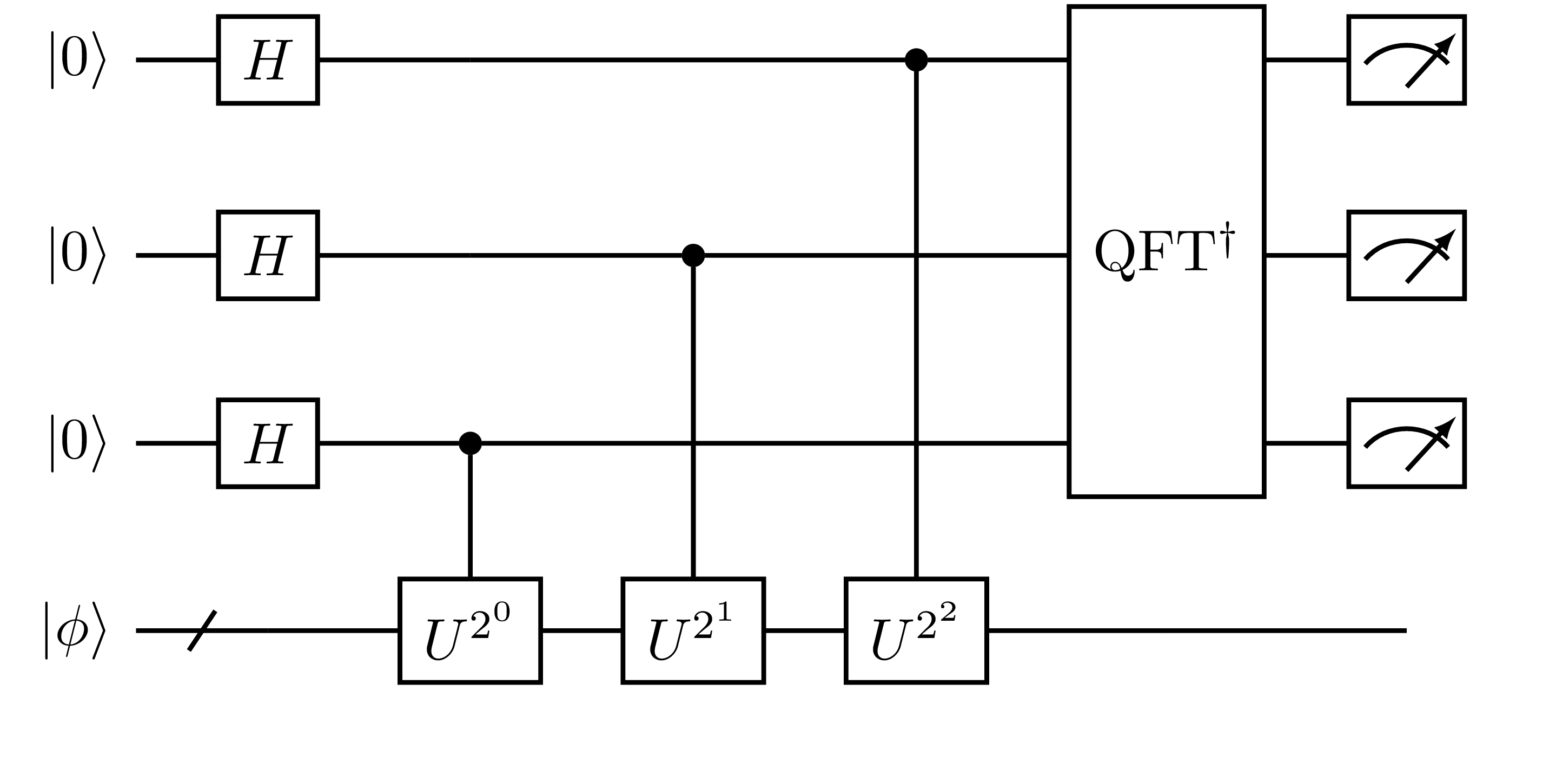
Fig. 4 Example of the canonical QPE circuit with three ancilla qubits.

In chemistry, QPE is most often proposed within the context of calculating molecular energies. For this purpose, we set the unitary to the time evolution operator \(U(t) = e^{-iHt}\), where \(H\) is the Hamiltonian describing the system. \(t \in \mathbb{R}\) is a parameter. Then, the eigenstate energy is obtained as \(E = -2\pi\phi / t\). The initial state is chosen to be some trial electronic wavefunction \(|\Phi\rangle\), such as the Hartree-Fock state. The “quality” of the initial state is an important factor to obtain the target phase value efficiently, as the probability of obtaining \(\phi\) is dependent on the overlap \(\langle \phi | \Phi \rangle\). One can also use an ansatz that has been optimized, such as by VQE, which may lead to a reduction in the overall computational time.

AlgorithmDeterministicQPE may be used for performing the canonical QPE algorithm. The phase estimation circuit requires subcircuits which perform repeated sequences of the unitary evolution operator controlled upon the ancilla qubits. We refer to one of these sequences as \(\mathrm{ctrl-}U\). Here, to prepare \(\mathrm{ctrl-}U\) from the molecular Hamiltonian \(H\), we follow the same steps as those for AlgorithmVQE.

from inquanto.express import get_system
from inquanto.mappings import QubitMappingJordanWigner

target_data = "h2_sto3g.h5"
fermion_hamiltonian, fermion_fock_space, fermion_state = get_system(target_data)
mapping = QubitMappingJordanWigner()
qubit_hamiltonian = mapping.operator_map(fermion_hamiltonian)

Currently, InQuanto supports the Suzuki-Trotter decomposition to construct the \(\mathrm{ctrl-}U\) circuit (shown in the cell below). Several methods have been proposed in the literature with different asymptotic scaling, such as quantum signal processing. [17]

# Generate a list of qubit operators as exponents to be trotterized.
qubit_operator_list = qubit_hamiltonian.trotterize(trotter_number=1)

# The parameter `t` that is physically recognized as the time period in atomic units.
time = 1.5

The initial state \(|\Phi\rangle\) is provided as a non-symbolic ansatz. The example below uses a modestly optimized UCCSD ansatz for our initial state preparation circuit.

from inquanto.ansatzes import FermionSpaceAnsatzUCCSD

# Preliminary calculated parameters.
ansatz_parameters = [-0.107, 0., 0.]

# Generate a non-symbolic ansatz.
ansatz = FermionSpaceAnsatzUCCSD(fermion_fock_space, fermion_state, mapping)
parameters = dict(zip(ansatz.state_symbols, ansatz_parameters))
state_prep = ansatz.subs(parameters)

A list of qubit operators thus generated is passed to the constructor of AlgorithmDeterministicQPE as

from inquanto.algorithms import AlgorithmDeterministicQPE

algorithm = AlgorithmDeterministicQPE(
    state_prep,
    qubit_operator_list * time,
)

Then, we build a protocol to construct a canonical QPE circuit. n_rounds specifies the number of ancilla qubits of the first quantum register, which determines the precision of the computation. Together with the four qubit representation hydrogen molecule state the circuits have a total of eight qubits.

from pytket.extensions.qiskit import AerBackend
from inquanto.protocols import CanonicalPhaseEstimation

# Choose the backend.
backend = AerBackend()

# Set the number of rounds (ancilla qubits of the first quantum register)
n_rounds = 4

# Chose the protocol to specify how the circuit is handled.
protocol = CanonicalPhaseEstimation(
    backend=backend,
    n_rounds=n_rounds,
    n_shots=10,
)

# Build the algorithm to get it ready for experiments.
algorithm.build(
    protocol=protocol,
);

Now the circuit is run by algorithm.run() to produce the final results. The algorithm.final_energy() returns the energy estimate.

# Run the protocol.
algorithm.run()

# Display the final results.
energy = algorithm.final_energy(time=time)
print(f"energy estimate  = {energy:8.4f} hartree")

energy estimate  =  -1.1667 hartree