Protocols for overlap squared

The OverlapSquared, or fidelity, of two quantum states \(\ket{\Psi_0}\) and \(\ket{\Psi_1}\) is given by:

(42)\[|\langle \Psi_0 | \Psi_1 \rangle |^2\]

Shot-based calculations of the overlap squared are supported by three InQuanto protocols: ComputeUncompute, SwapTest, and DestructiveSwapTest. In all cases one may calculate the bare fidelity, as above, or with a kernel consisting of a single Pauli string:

(43)\[|\langle \Psi_0 | h P | \Psi_1 \rangle |^2\]

where \(h\) is a scalar factor. All of these protocols use a single quantum circuit to perform the measurement.

ComputeUncompute

Let \(\ket{\Psi_0} = U_0 \ket{\bar{0}}\) and \(\ket{\Psi_1} = U_1 \ket{\bar{0}}\), where \(U_0\) and \(U_1\) are state preparation unitaries. The fidelity is hence given by \(|\langle \bar{0} | U_0^\dagger U_1 | \bar{0} \rangle |^2\). The ComputeUncompute protocol prepares the state \(U_0^\dagger U_1 \ket{ \bar{0}}\) directly by concatenating the state preparation unitaries (“computing” the \(\ket{\Psi_1}\) state and “uncomputing” \(\ket{\Psi_0}\)) [27], generating a circuit of the form:

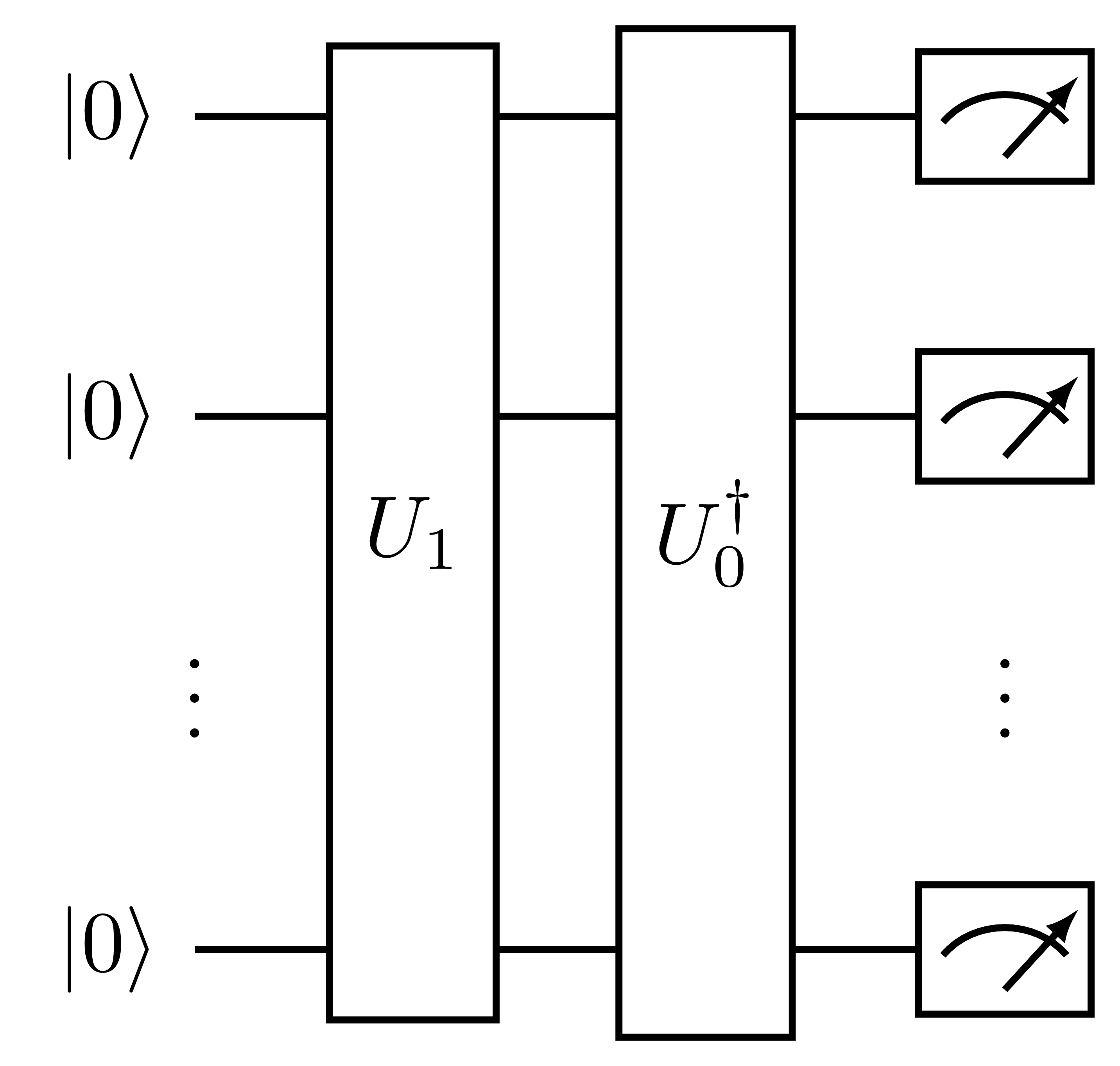
Fig. 11 Measurement circuit generated by ComputeUncompute.

The full register is measured in the computational basis, and the overlap squared is given by the probability of measuring all qubits in the zero state, \(\ket{\bar{0}}\). See a simple example below:

from sympy import sympify
from inquanto.operators import QubitOperator, QubitOperatorList
from inquanto.states import QubitState
from inquanto.ansatzes import TrotterAnsatz
from inquanto.computables import OverlapSquared
from inquanto.protocols import ComputeUncompute
from pytket.extensions.qiskit import AerBackend

reference = QubitState([1, 1, 0, 0])
theta0, theta1 = sympify("theta0"), sympify("theta1")

ansatz0 = TrotterAnsatz(
   QubitOperatorList(QubitOperator("Y0 X1 X2 X3", 1j), theta0),
   reference
)

ansatz1 = TrotterAnsatz(
   QubitOperatorList(QubitOperator("X0 Z1 Y2 Z3", 1j), theta1),
   reference
)

fidelity = OverlapSquared(ansatz0, ansatz1)

protocol = ComputeUncompute(AerBackend(), n_shots=1000)
protocol.build_from({theta0: -0.111, theta1: 2.5}, fidelity)
protocol.run(seed=0)

circuit = protocol.get_circuits()[0]
print("Circuit depth: ", circuit.depth())
print("Num qubits: ", circuit.n_qubits)

fidelity.evaluate(protocol.get_evaluator())

Circuit depth:  19
Num qubits:  4

0.634

SwapTest

The SwapTest protocol implements the canonical swap test for evaluating the overlap squared [28]. This procedure prepares both states in parallel registers and performs a SWAP operation between them, controlled on an ancilla qubit in the \(\ket{+}\) state. In general, this circuit takes the form:

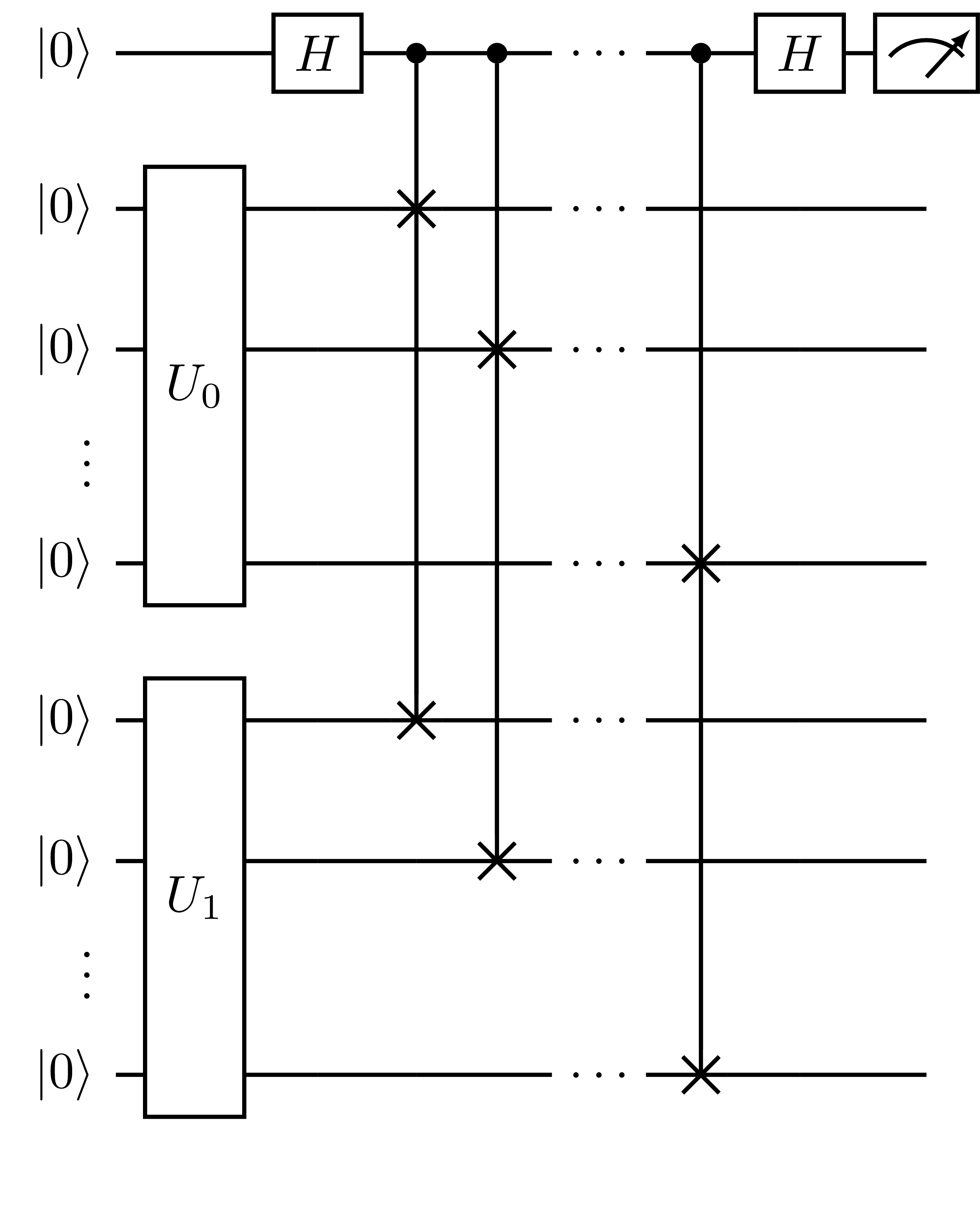
Fig. 12 Measurement circuit generated by SwapTest.

The probability of measuring the ancilla qubit in the \(\ket{0}\) state is then given by \(p(0) = \frac{1}{2}(1 + |\langle \Psi_0|\Psi_1 \rangle|^2)\), from which the overlap squared is extracted. Similarly to above, this protocol is used as follows:

from inquanto.protocols import SwapTest

protocol = SwapTest(AerBackend(), n_shots=1000)
protocol.build_from({theta0: -0.111, theta1: 2.5}, fidelity)
protocol.run(seed=0)

circuit = protocol.get_circuits()[0]
print("Circuit depth: ", circuit.depth())
print("Num qubits: ", circuit.n_qubits)

fidelity.evaluate(protocol.get_evaluator())

Circuit depth:  45
Num qubits:  9

0.6499999999999999

DestructiveSwapTest

Similarly to the SwapTest, the DestructiveSwapTest prepares both states in parallel registers, but does not require an ancilla qubit. This method performs an effective XOR operation between the states by appending a ladder of CNOT gates between the i-th qubits of each register, and a layer of Hadamard gates on the control register [29]. In general, this circuit takes the form:

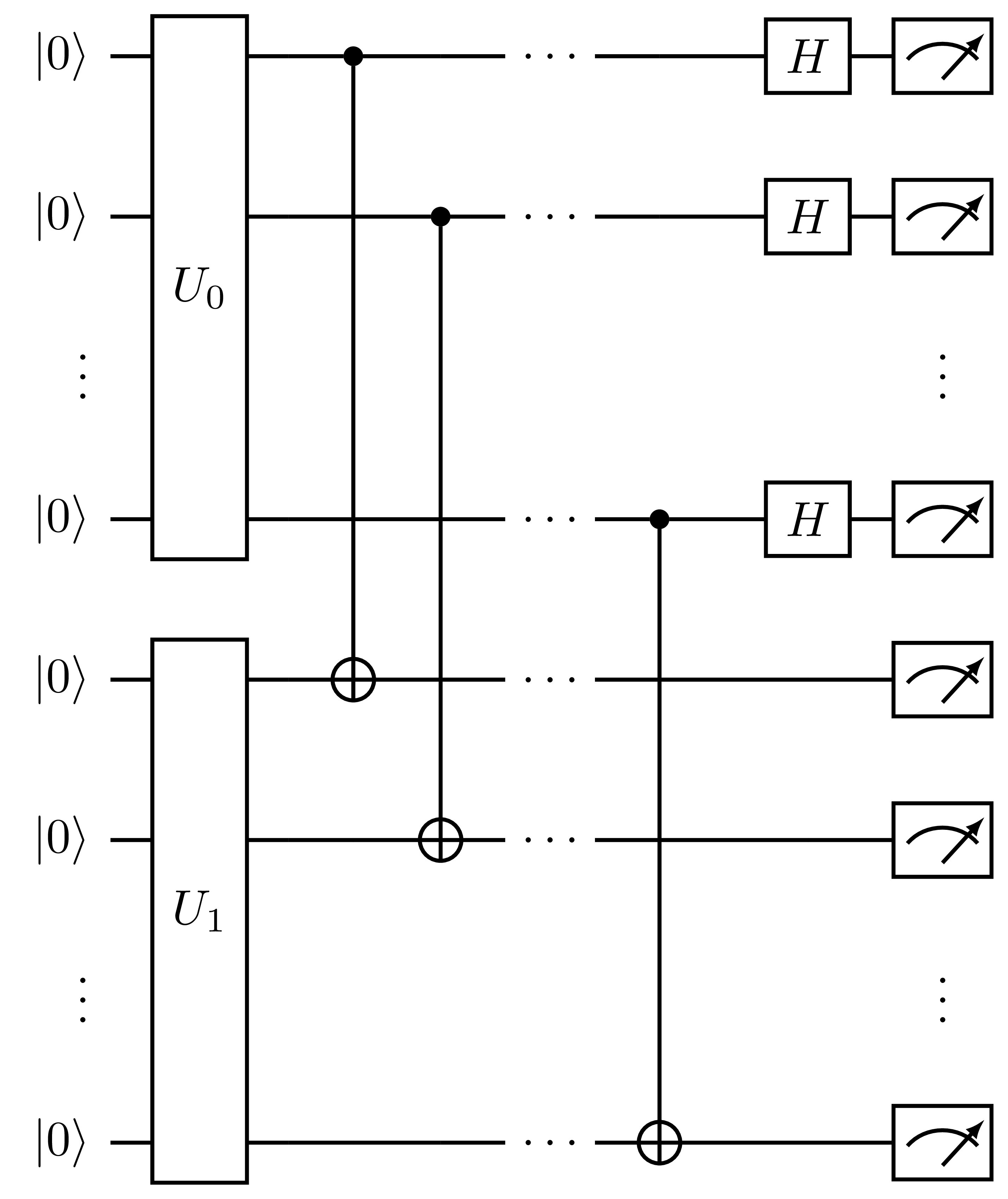
Fig. 13 Measurement circuit generated by DestructiveSwapTest.

The total phase shift between the states is given as \(\pi \sum_{i=1}^n M_i^1 M_i^2\), where \(M_i^r\) is the measurement outcome on the i-th qubit of the first or second state register. A particular shot is deemed successful if the bitwise AND operation between the two state registers has even parity. The probability of success is given by \(p_s = \frac{1}{2}(1 + |\langle \Psi_0|\Psi_1 \rangle|^2)\), from which the overlap squared is computed. Similarly to above, this protocol is used as follows:

from inquanto.protocols import DestructiveSwapTest

protocol = DestructiveSwapTest(AerBackend(), n_shots=1000)
protocol.build_from({theta0: -0.111, theta1: 2.5}, fidelity)
protocol.run(seed=0)

circuit = protocol.get_circuits()[0]
print("Circuit depth: ", circuit.depth())
print("Num qubits: ", circuit.n_qubits)

fidelity.evaluate(protocol.get_evaluator())

Circuit depth:  12
Num qubits:  8

0.6439999999999999